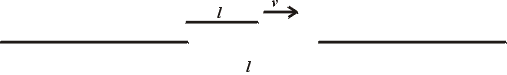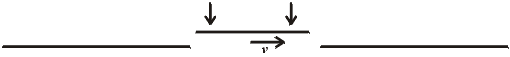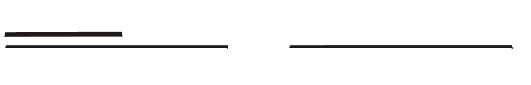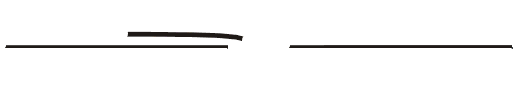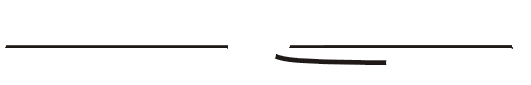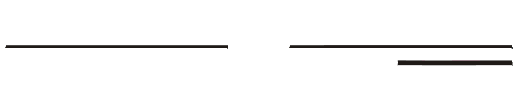Úvod
Úvod

Sepětí prostoru a času v jediném čtyřrozměrném kontinuu, v tzv. prostoročasu,
vede k tomu, že prostorové události a časové intervaly mezi dvěma událostmi posuzovány
ve dvou inerciálních vztažných soustavách, tedy soustavách naprosto rovnoprávných, se jeví
různě a výsledky jsou zdánlivě neslučitelné.
Za paradoxní označujeme právě ty situace, kdy dva, oba přesvědčivě získané výsledky sobě
odporují. Řešení je téměř vždy třeba hledat v chybné a nekorektní formulaci problému
či v zamlčeném a neuvědomělém přijetí zdánlivě samozřejmého, avšak ve skutečnosti
nesplněného předpokladu.

 Paradox transportéru
Paradox transportéru
Sledujme transportér podle obr.6.
Na transportéru délky L0 je umístěn gumový pás dvojnásobné délky 2L0.
Můžeme předpokládat, že transportér je dostatečně dlouhý tak, abychom vlivy otáčejících se kol na obou koncích mohli zanedbat. Hmotnost pásu nechť je rovněž malá, abychom mohli přehlédnout dynamické efekty na koncích, spjaté se změnou směru pohybu pásu. Rychlost nechť je relativistická.
Transportér má v soustavě S, spjaté s rámem, délku L0. Horní i dolní část pásu se však vůči této soustavě pohybuje, každá by tedy měla podléhat kontrakci faktorem
Ö(1 - b2) , b = v/c.
Délka pásu za pohybu by měla být
l = 2L0 Ö(1 - b2) < 2L0.
Zkrátí se pás při svém pohybu ?
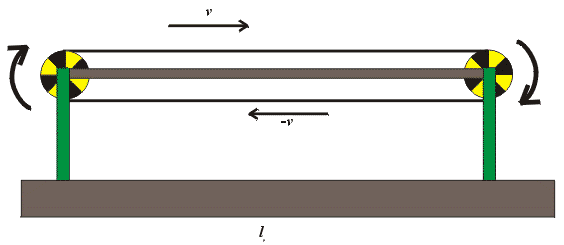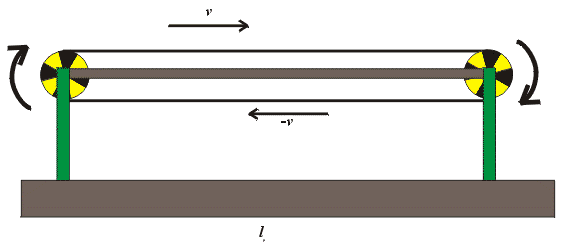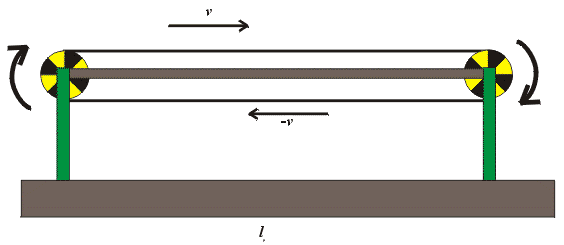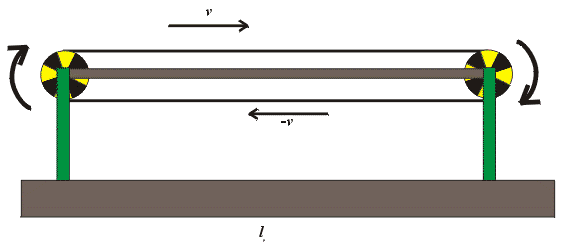
Obrázek 6
Samozřejmě, že provést detailní analýzu bez započtení efektů na obou koncích nelze. Argument, že mnohonásobné prodloužení délky transportéru zvětšuje mnohonásobně efekt kontrakce délky, zatímco efekty na koncích zůstávají neměnné, je přesvědčivý a dokládá, že vlivy na obou koncích by neměly být v analýze rozhodující.
Situace je paradoxní a zdá se odporovat relativistické kontrakci délek.
Únik z paradoxu spočívá v uznání, že pohybující se pás není na transportéru sice zkrácen, je však napjat. V pásu se při pohybu objeví silové působení a pás se potřebně prodlouží. Překročí-li rychlost jistou mez závislou na materiálu pásu, pás se přetrhne a transportér nemůže fungovat. Ostatně, s tuhostí a pružností těles v relativitě to vůbec není prosté, jak dokládají četné jiné známé paradoxy (Rovnováha a nerovnováha na tuhé páce, Síla v dokonale ohebném vlákně a jiné).

 Paradox rychlého chodce
Paradox rychlého chodce
aneb
paradox tyče a otvoru
Velmi populární paradox, založený na jevu kontrakce délek, může být formulován jako otázka, zda velmi rychlý chodec (a tedy hodně zkrácený ve směru své chůze) spadne do pouličního kanálu, přes který má přejít.
Fyzikálnější formulace úlohy může být podána takto :
Tenká tyč metrové délky se posouvá velkou rychlostí podél hladké vodorovné desky s otvorem právě velikosti jednoho metru,
Z hlediska soustavy spojené s deskou se jeví tyč zkrácena podle obr.7 a můžeme očekávat, že do otvoru propadne. Z hlediska soustavy , spjaté s pohybující se tyčí se však jeví podle obr.8 situace tak, že přední konec tyče přesáhne za otvor dávno před tím, než zadní část tyče nad otvor vstoupí (obr.8), takže by tyč do otvoru spadnout neměla. Propadne tyč do otvoru? Ano nebo ne? A proč ?
Obrázek 7
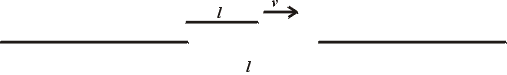
Obrázek 8

K tomu, aby tyč propadla, je třeba jisté (byť i jen velmi slabé) síly, nutící tyč k pohybu dolů. Abychom se vyhnuli otázkám po gravitační síle a tím i po eventuální potřebě při analýze úlohy použít obecné teorie relativity, doplňme formulaci tak, že okamžiku, kdy se tyč nachází nad otvorem podle obr.7 ťukneme současně na oba konce tyče směrem dolů, takže tyč propadne (obr.9). Podle obr.8 se však nezdá, že by to pomohlo.
Obrázek 9
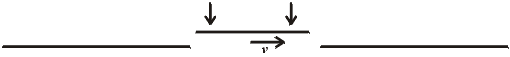
Ošidné je ono "současné" ťuknutí na oba konce. Současnost není absolutní a tak bližší analýza by ukázala, že nejprve bylo ťuknuto na její přední konec a teprve poté na její konec zadní. Tyč se tedy vlivem těchto následných ťuknutí nakloní a otvorem projde.
Abychom odstranili "současnost", ťukněme jen jednou a to přesně doprostřed. Jenže...Střed tyče (přesněji: střední událost, ležící mezi dvěma současnými událostmi na obou koncích tyče) není absolutní, závisí na vztažné soustavě, a tak, zatímco z hlediska S jsme ťukli doprostřed, z hlediska S' to uprostřed nebylo, tyč se opět nakloní a otvorem může projít. Nebudeme tyto změny formulace dále upravovat, upřesňovat a rozebírat, není to ani třeba. Zdá se však, že tyto modifikace nasvědčují tomu, že tyč otvorem projít může.
Korektní a bezproblémový závěr, že tyč do otvoru spadne, vyplývá z uvědomění si faktu, že v teorii relativity neexistují tuhé tyče. Přední konec tyče, jakmile vstoupí nad otvor, se ohne směrem dolů a tyč do otvoru klouzne obr.10.
Obrázek 10
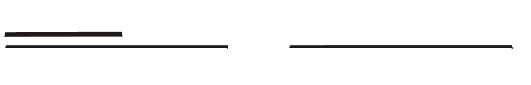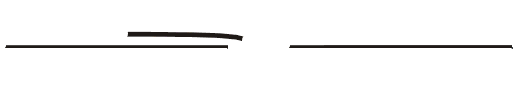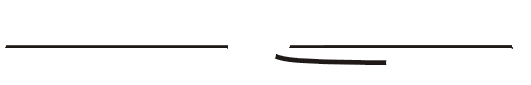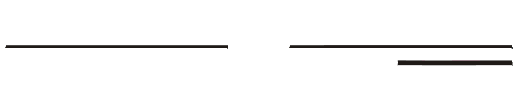
Neslučitelnost představy tuhé tyče s teorií relativity je patrná z obr.11. Úder na jeden konec tyče by se nutně musel projevit jejím pohybem jako celku a posunutí levého konce by okamžitě vedlo k posunutí jejího pravého konce. Takováto nekonečná rychlost přenosu signálu je však v teorii relativity nepřípustná. Každé posunutí se tyčí se šíří jako pružná vlna a to hluboce podsvětelnou rychlostí. V teorii relativity žádná tyč není tuhá. Pružné vlastnosti a tím i šíření se vzruchů prostředím jen omezenou rychlostí, jsou v teorii relativity nezbytné.

Obrázek 11
Poznámka: Tuto okolnost jsme, ostatně, potkávali již v paradoxu transportéru. Pás v pohybu mění svojí přirozenou, nenapjatou délku. Objevuje se v něm napětí a při velké rychlosti napětí nevydrží a přetrhne se.
Snad ještě ostřeji se tento jev objevuje v tzv. paradoxu roztočeného kola podle obr.12.

|
Obrázek 12
|
Obvod kola by se měl, posuzováno z klidné soustavy, kontrakcí délek ve svém pohybu zkrátit, zatímco poloměr R, jehož směr je ke směru pohybu kolmý a kontrakci nepodléhá, by měl zůstat nezměněn.
Dostáváme se až k otázce : Platí vůbec O=2pR ? V roztočeném kole se nutně objeví napětí a při příliš rychlém pohybu se kolo deformuje nebo dokonce praskne. Tato úloha by nás však zavedla až k otázkám "zdánlivých sil", k síle gravitační a k problémům neeuklidovské geometrie. To by překročilo meze paradoxu ze speciální teorie relativity.

 Paradox zhasnuté žárovky
Paradox zhasnuté žárovky
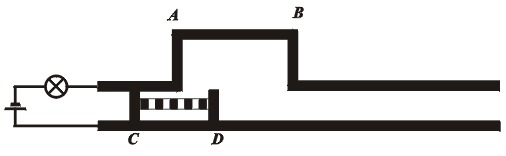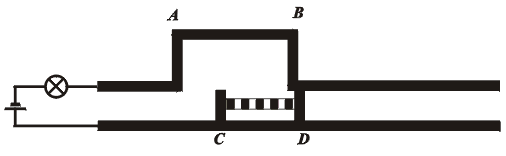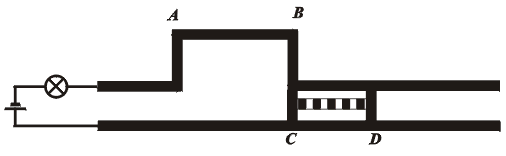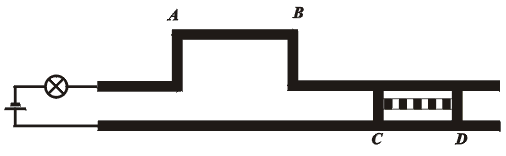
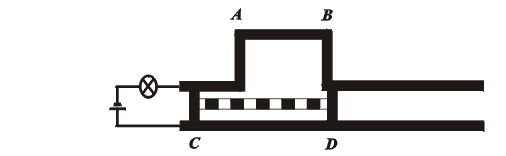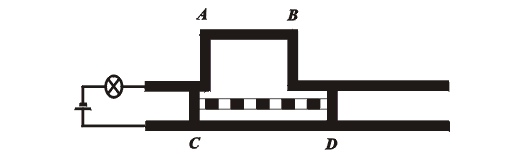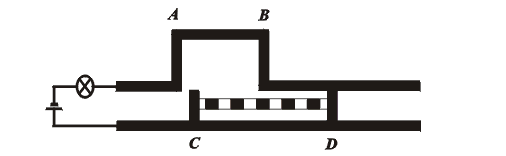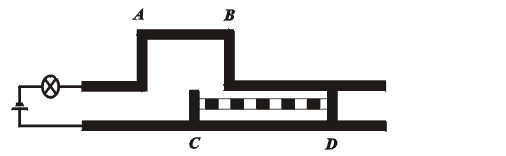
Jezdec ve tvaru H (s nevodivou příčkou mezi oběma vodivými rameny) se pohybuje velkou rychlostí podél rovnoběžných vodičů spojených s baterií a žárovkou podle přiloženého obrázku.
Z pohledu vztažné soustavy S spjaté s "kolejemi" je v důsledku kontrakce délky CD kontakt dočasně přerušen a žárovka na chvíli zhasne (obr.13). (CD < AB).
Z pohledu jiné inerciální soustavy S´, spjaté s jezdcem, je naopak zkrácena vzdálenost AB (délka, v níž je vzdálenost mezi vodiči poněkud zvětšena), takže kontakt v obvodu se žárovkou nikdy přerušen není (CD > AB). Žárovka tedy může svítit trvale.(obr.14)
Zhasne žárovka? Ano nebo ne? Vysvětlete.
Z hlediska soustavy S' by zhasnutí mělo být dokonce relativisticky prodlouženo (tzv. diletace času). Zkuste i vypočítat.
Obrázek 13
Obrázek 14

Mezi další četné paradoxy teorie relativity patří zejména tzv. paradox času (neboli paradox dvojčat), různé paradoxy z relativistické elektrodynamiky, i mnoho dalších paradoxů vznikajících ze sepětí prostoru a času.
Formulace, zvládnutí a řešení paradoxů má pro vyučování významné naukové a výchovné hodnoty. Odhaluje nekorektní a nekonzistentní formulace, chybné a zamlčené předpoklady a předsudky a přivádí k hlubšímu porozumění a proniknutí do ducha rozebírané teorie.